Введение. Тема причинности является одной из важнейших и дискуссионных в эпидемиологии; однако, до сих пор не существует единого определения причинности, принятого научным сообществом [1, 2]. В исследовании Parascandola and Weed [3], опубликованном в 2001 году был проведен анализ 148 публикаций с целью выявить, как эпидемиологи трактуют понятие причинность. Авторы показали, что в эпидемиологической литературе используется пять основных категорий определений причинности, каждая из которых имеет свои достоинства и недостатки. В результате, была предложена классификация определений причинности, согласно которой, результат не может произойти без Необходимой Причины (necessary cause) и наличия этой причины достаточно для наступления эффекта. Развитием предыдущего определения может выступать Достаточное количество компонентов (sufficient-component cause), ситуация, при которой каждый из компонентов причины по отдельности не является достаточным для наступления эффекта, но их комбинация приводит к результату. Определение Действие (production) описывает ситуацию, когда причина – это то, что производит эффект (следствие). Причина увеличивает вероятность возникновения результата в соответствии с определением вероятностной причинности (probabilistic cause). Согласно контрфактическому определению (counterfactuals), наблюдаемый эффект при наличии причины отличается от эффекта, который имел бы место, если бы причина была бы другой или даже отсутствовала.

Чтобы различать причинную и непричинную связь, Austin B. Hill [4] предложил следующие критерии: 1) сила связи, 2) постоянство ассоциации, 3) специфичность, 4) временной характер, 5) биологический градиент, 6) правдоподобие (биологическое правдоподобие), 7) согласованность, 8) эксперимент и 9) аналогия.

Знание того, является ли тот или иной фактор риска причинно-значимым занимает центральное место в разработке лекарственных препаратов, своевременной профилактике и терапии в доказательной медицине; источниками этих знаний служат результаты эпидемиологических исследований. При этом, стандартные наблюдательные исследования имеют ограниченные возможности оценки причинно-следственной связи между воздействием (фактором риска) и исходом (клиническим состоянием), поскольку смещение оценки [5] и обратная причинно-следственная связь [6] могут привести к систематической ошибке. Это отражено в высказывании: «ассоциация не означает каузации или причинно-следственной связи».

Рандомизированные контролируемые исследования (РКИ) считаются золотым стандартом при проведении медицинских исследований и важны для определения наличия причинно-следственной связи между фактором риска и исходом [7, 8]. Однако иногда проведение РКИ связано с рядом сложностей или просто невыполнимо (например, невозможно провести РКИ для оценки причинно-следственного влияния массы тела при рождении на развитие катаракты, неэтично проводить исследование какого-либо вмешательства с высоким риском развития осложнений). Поэтому, в ряде случаев имеется необходимость в применении других методов установления причинно-следственной связи.

Теоретические основы метода Менделевской рандомизации

Менделевская рандомизация (МР) – это способ исследования, в котором генетический вариант (полиморфизм, SNP) используются в качестве инструментальной переменной для установления и количественной оценки причинно-следственной связи между модифицируемым фактором риска и интересующим исследователя фенотипическим признаком (чаще всего, заболеванием).  Возможность оценки влияния уровня холестерина крови на риск развития онкологической патологии с помощью генетической информации (носительство «холестерин-снижающего» аллеля гена Аполипротеина Е [APOE]) была предложена Катаном в 1986 году [9].  Автор сделал заключение, что вследствие независимого распределения генов, группа лиц со «снижающим холестерин» аллелем и группа носителей другого аллеля будут однородными, то есть между группами не будет никаких систематических различий, обусловленных вмешивающимися факторами. Сравнение распределения аллелей APOE у лиц с онкологическими заболеваниями с таковым у здоровых людей позволяет, в таком случае сделать вывод о наличии или об отсутствии причинно-следственной связи между низким уровнем холестерина и риском развития рака. Впервые термин «Менделевская рандомизация» был использован Греем и Уитли [10] и стал известен широкому кругу эпидемиологов после выхода публикации Дж. Дейви Смита и Эбрахима [11].

Метод инструментальных переменных (instrumental variables) как научный подход нашел широкое применение в экономических науках, применяется для решения проблемы эндогенности, в том числе из-за обратной причинно-следственной связи и корреляции регрессоров со случайной составляющей. Инструментальная переменная или инструмент — это переменная, которая коррелирует c воздействием (предиктором), но не коррелирует с исходом (переменной отклика, рис. 1). Для того, чтобы переменная Z была валидным (допустимым) инструментом, она должна соответствовать следующим критериям:

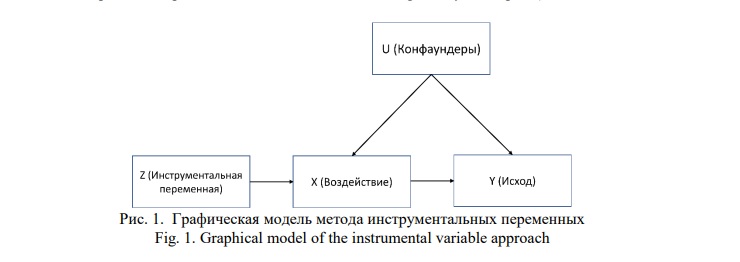
1) Коррелировать с воздействием X (релевантность, relevance)

2) Влиять на результат только через воздействие (исключающее ограничение, exclusion restriction)

3) Не иметь общей причины с исходом Y (независимость, independence или exchangeability assumption)

Критерии валидности инструментальной переменной применимые к генетическому варианту в Менделевской рандомизации выглядят следующим образом (рис. 2):

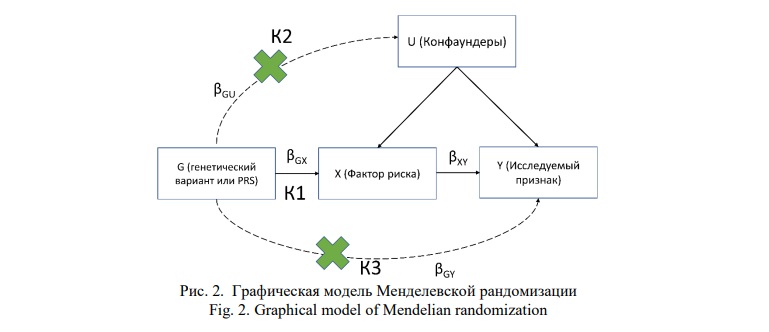
1) К1 на рисунке 2. Значимая корреляция генетического варианта с фактором риска развития исследуемого признака. Благодаря тому, что результаты большинства полногеномных исследований ассоциаций (GWAS) находятся в свободном доступе, поиск таких вариантов не является сложной задачей. Принято использовать генетические варианты, связанные с фактором риска с «полногеномным» уровнем значимости (р <5 x 10 ^-8).

2) К2 на рисунке 2. Отсутствие корреляции с вмешивающимися факторами ассоциации фактором риска с исследуемым признаком ( , важно отметить, что - в данном случае не корреляция, а регрессионный коэффициент, который совпадает с корреляцией только в одномерном случае.

3) К3 на рисунке 2. Генетический вариант должен оказывать воздействие на исследуемый признак только через фактор риска. Это означает, что частная корреляция между G и Y при фиксированном X равна 0. В этом случае rGY = rGX× rYX, что и отражено в формуле 1.

Проверка соответствия генетического варианта второму и третьему критерию практически невозможна; исследователи вынуждены действовать методом «от обратного», т.е. опровергать несоответствие [12]. Для получения достоверной оценки причинности ассоциации в случае, если некоторые из генетических вариантов не являются валидным инструментальными переменными используется ряд анализов чувствительности, разработанных в последнее время [13, 15].

Среди основных причин несоответствия генетических инструментов критериям валидности стоит отметить плейотропию. Генетические варианты, связанные с развитием нескольких признаков, называются плейотропными и их применение в МР анализе нежелательно из-за несоответствия второму или третьему критерию. Если плейотропия возникает в результате корреляции варианта с каким-либо промежуточным фенотипом, который, в свою очередь влияет на исследуемый признак, то такое явление называется вертикальной плейотропией [16]. В случае вертикальной плейотропии генетический вариант может использоваться как инструментальная переменная.  Если влияние полиморфизма на исследуемый признак осуществляется через два или более независимых механизма, то речь идет о горизонтальной плейотропии и такой полиморфизм не соответствует критериям валидности и не может быть использован в качестве инструментальной переменной. Направленная плейотропия возникает в случае смещения оценки эффекта в одном направлении, если же средний плейотропный эффект равен нулю, то такая плейотропия называется сбалансированной. В последнее время разработан ряд статистических методов, позволяющих провести тест на наличие плейотропии, которые широко используются в качестве анализов чувствительности при проведении Менделевской рандомизации [17].

Менделевская рандомизация и рандомизированные контролируемые исследования

В МР анализе исследователи делают допущение что распределение аллелей независимо от различных вмешивающихся факторов, т.е. является случайным. Действительно, трудно представить, что уровень дохода или образования человека во взрослом возрасте могут оказывать влияние на то, носителем какого аллеля этот индивид является. Важным исключением является этническая принадлежность: частоты аллелей могут значительно различаться в разных популяциях, приводя к тому, что аллели, ассоциированные с фактором риска, могут быть связаны с различными уровнями вмешивающихся факторов.

При проведении рандомизированных контролируемых исследований, баланс прогностических факторов (известных и неизвестных) при назначении лечения обеспечивается благодаря независимому распределению пациентов в основную и контрольную группы. Независимое распределение аллелей во время мейоза позволяет провести аналогию межу рандомизированными контролируемыми исследованиями и МР (рис. 3).

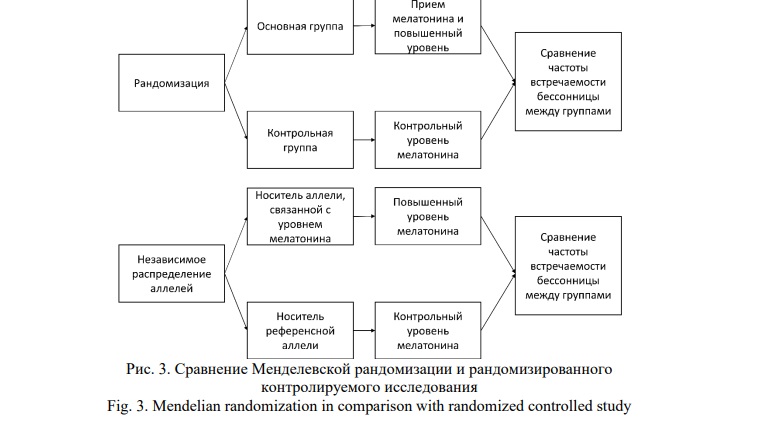
Количество инструментальных переменных

В ряде ранних публикаций МР анализов исследователи использовали один генетический вариант с изученным биологическим механизмом, объясняющим изменения в факторе риска. Примером может послужить работа научного коллектива, под руководством Timpson [18], в которой исследовалась роль избыточной массы тела в развитии артериальной гипертензии. Авторы использовали единственный полиморфизм rs9939609 гена FTO, ассоциированный с ожирением у детей и взрослых. Действительно, значение этого генетического варианта в развитии ожирения было показано в ранее проведенных исследованиях, кроме того, доля дисперсии индекса массы тела, объясненная этим полиморфизмом, составила по оценкам разных авторов от 0,24 до 1%, что подтверждает правильность выбора инструментальной переменной.

В случае с одной инструментальной переменной, эффект фактора риска на исследуемый признак может быть представлен, как частное эффекта инструмента на исследуемый признак и эффекта инструмента на фактор риска (формула 1).

                                                                                                                            (1)

В ряде случаев, исследователи применяют в качестве единственного инструмента индекс полигенного риска (Polygenic risk score; PRS), суммируя количество аллелей, связанных с фактором риска в каждом из генетических вариантов для каждого участника выборки (невзвешенный индекс) или используя степень ассоциации риск-аллеля как взвешивающий коэффициент (взвешенный индекс риска, формула 2) [19].

                                                            =                                                (2)

где B_j – это коэффициент регрессии фактора риска на генетический вариант j,

Npa – количество риск-аллелей у варианта j у участника i.

Другим статистическим методом, используемым при работе с единственным генетическим инструментом, является двухшаговый метод наименьших квадратов (двухшаговый МНК). На первом шаге оценивается регрессия фактора риска (переменной Х) по инструменту (переменная G, формула 3). В результате получаем предсказанные значения .

                                                              (3)

На втором шаге оценивается регрессия исследуемого признака (переменная Y, формула 4) по предсказанным значениям .

                                                                (4)

Оценка  будет состоятельной вследствие экзогенности .

Однако, в большинстве случаев, доля дисперсии фенотипа, объясненная одним полиморфизмом мала, приводя к смещению оценки из-за наличия «слабых» инструментов [20]. Тест на слабые инструменты соответствует значению F-статистики первого шага 2МНК, так при значении F-статистики больше 10 делается вывод о релевантности инструмента. Чтобы избежать смещения оценки при слабости инструмента были разработаны статистические методы, позволяющие использовать несколько (или много) полиморфизмов, увеличивая как долю дисперсии фактора риска, объясненного генетическими вариантами, так и мощность исследования. При использовании множества инструментов, сначала оценивается индивидуальный эффект каждого из них, затем проводится метаанализ этих оценок эффекта ( , формула 1) с использованием метода взвешенных значений обратной дисперсии. Взвешивающим коэффициентом служит обратная дисперсия ассоциации SNP – исход ( ). В настоящее время насчитывается не менее 47 статистических методов, используемых при проведении МР анализа, каждый из которых имеет свои особенности и области применения [21].

МР на одной или на двух выборках

Менделевскую рандомизацию может быть проведена с использованием одной или двух выборок. В первом случае, инструменты выбираются на основании ранее проведенных полногеномных анализов ассоциации, а степень корреляции этих полиморфизмов с фактором риска и ассоциация фактора риска с исходом определяется на одной выборке. Для этого типа исследования необходим доступ к индивидуальной гено- и фенотипической информации каждого участника выборки, кроме этого, для достижения необходимой статистической мощности исследования необходимо проводить МР анализ на достаточно большой выборке.  Если для оценки корреляции инструмента с фактором риска используется одна выборка, а для оценки корреляции с исследуемым признаком другая, то речь идет о МР на двух выборках. Сначала отбираются полиморфизмы, значимо ассоциированные с фактором риска по результатам полногеномного исследования ассоциаций, когда в качестве источника данных служит сводная статистика GWAS или метаанализов полногеномных исследований, проведенных на больших выборках. Критериями отбора обычно служат уровень значимости ассоциации не выше 5 × 10^-8, частота минорного аллеля не ниже 5%, значения коэффициента корреляции r² Пирсона для неравновесия по сцеплению не выше 0,05. Далее, необходимо получить регрессионные коэффициенты, полученные для отобранных SNP в сводной статистике полногеномного исследования ассоциаций исхода (рис. 4). В этом случае уровень значимости ассоциации полиморфизма с исследуемым признаком не является критерием, влияющим на проведение анализа.

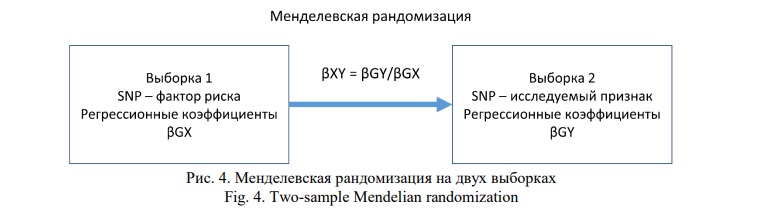
Проведение МР на двух выборках позволяет проверять значительно большее количество гипотез, чем одновыборочная МР. Среди источников сводных данных полногеномных исследований, пожалуй, основным является GWAS Catalog [22] (https://www.ebi.ac.uk/gwas/summary-statistics), содержащий по состоянию на 30 сентября 2022 года информацию о 6004 публикациях и 423182 ассоциациях. Другим важным ресурсом является проект Университета Бристоля IEU open GWAS project (https://gwas-api.mrcieu.ac.uk/), с интегрированной возможностью провести МР анализ в онлайн-режиме [23,24].

Однако, следует помнить, что обе выборки должны быть схожими по этнической принадлежности вследствие наличия этнических особенностей в распределении частот аллелей полиморфных маркеров.

Среди основных программных средств для проведения Менделевской рандомизации на двух выборках стоит отметить библиотеки TwoSampleMR и MendelianRandomization в среде R. Данные библиотеки также позволяют пользователю провести ряд анализов чувствительности и визуализировать полученные результаты. В среде Stata используются библиотеки ivonesamplemr, ivreg2. Для МР анализа на одной выборке применяются библиотеки ivmodel, ivtools и AER в среде R и mrrobust  в среде Stata

Нелинейная Менделевская рандомизация

Оценка эффекта при проведении Менделевской рандомизации может быть малоинформативной в случае нелинейной модели взаимосвязи между исходом и фактором риска. С помощью данного метода можно оценить варьируется ли эффект воздействия на оцениваемый признак в зависимости от уровней воздействия, т.е. является ли эффект дозозависимым. Для проведения нелинейной МР был предложен ряд методов, включая полиномиальный (fractional polynomial) и кусочно-линейный (peacewise linear) регрессионный анализ [25].

Нелинейная МР применялась для исследования линейности взаимосвязи антропометрических признаков и ряда заболеваний на выборке Британского биобанка [26]. Результаты этого интересной работы свидетельствуют, что в подавляющем большинстве (84%) случаев, оцениваемая корреляция была нелинейной. Aravantis и соавторы [27]  провели оценку ассоциации диастолического артериального давления с сердечно-сосудистыми заболеваниями. В отличие от результатов обсервационных исследований, свидетельствующих о наличии J- образной ассоциации, данный МР анализ не подтвердил гипотезу о наличии нелинейной ассоциации. Среди других примеров применения нелинейной МР стоит отметить два исследования, проведенных в Британском биобанке. Это изучение причинно-значимой ассоциации индекса массы тела со смертностью [28], а также оценка роли дефицита витамина Д в развитии сердечно-сосудистых заболеваний [29]. Результаты этих работ позволяют сделать вывод о нелинейном характере ассоциации фактора риска с исходом в обоих случаях.

Многофакторная Менделевская рандомизация

Это вид МР анализа, в котором оценивается влияние нескольких факторов риска на исход, и в качестве инструментов используются генетические варианты, ассоциированные с этими факторами риска. Критерии валидности инструментальной переменной в таком случае выглядят, как: корреляция инструмента с каждым из воздействий, влияние на исход только через воздействия и отсутствие общей причины с исходом. Многофакторная МР может быть проведена на одной или на двух выборках [30] и особенно актуальна в случаях наличия двух или более коррелированных факторов риска для установления причинно-значимой роли каждого из этих факторов. Примером подобных факторов риска являются липиды плазмы крови, с ярко выраженной плейотропией генетических вариантов, ассоциированных сразу с несколькими фракциями липидов. В работе Richardson и соавторов [31] оценивалось влияние липидов плазмы крови на ишемическую болезнь сердца. Исследователи получили доказательства того, аполипопротеин В является ведущим фактором ассоциации липидов с ИБС. В другом исследовании изучалась связь липидов с повышенным риском развития рака молочной железы [32]. Было показано, что генетически детерминированные повышенные уровни ЛПВП и ЛПНП связаны с более высоким риском заболевания.

Двунаправленная Менделевская рандомизация

При проведении двунаправленного (bidirectional) МР анализа исследование проходит в два этапа. На первом этапе оценивается эффект фактора риска на исход, на втором этапе они «меняются местами», т.е. фактор риска становится исследуемым признаком, позволяя установить направление причинно-следственной связи с использованием генетических вариантов, значимо связанных с каждым признаком по результатам полногеномных исследований ассоциаций. Например, при объяснении наблюдаемой взаимосвязи между образованием и близорукостью может быть неясно, является ли более высокий уровень образования причиной или же нарушение зрения оказывает влияние на получаемое образование. Двунаправленная МР, проведенная в 2018 году, помогла ответить на этот вопрос, установив причинно-значимую роль образования на развитие миопической рефракции [33]. В другом исследовании изучалось что является причиной, а что следствием в ассоциации нарушений сна с психиатрическими заболеваниями [34]. Полученные результаты свидетельствуют о повышенном риске развития психических расстройств при серьезных нарушениях сна и о возможности использовать маркеры сна в диагностике cиндрома дефицита внимания с гиперактивностью и депрессии.

МР «свободная от гипотез»

Чаще всего МР применяется для тестирования гипотез о наличии причинно-следственной связи, однако, в ряде случаев интерес исследователя лежит в плоскости идентификации новых ассоциаций. Существуют примеры, когда эта стратегия показала многообещающие результаты в обнаружении предполагаемых причинно-следственных связей между фенотипами. В недавней работе Zheng и соавторов [35] изучалось влияние человеческого протеома на риск развития различных заболеваний. В результате было идентифицировано 111 причинно-значимых ассоциации между 62 протеинами и 52 фенотипами. Это исследование подчеркнуло возможности применения МР «свободной от гипотез» в получении более широкой картины взаимодействия фенотипов в отличие от традиционного подхода МР, когда оценивается эффект одного фактора риска на один исход.  В другом исследовании, проведённом в 2022 году [36] было установлено, что более ранний возраст наступления менопаузы связан с рядом заболеваний. Среди основных недостатков данного метода можно отметить необходимость поправки на множественную проверку гипотез и сложность в интерпретации результатов вследствие наличия плейотропии [37].

Когда можно провести Менделевскую рандомизацию

МР анализ рекомендуется применять в случаях, когда проведение клинических исследований затруднено или невозможно по разным причинам. Например, проведение рандомизированного исследования, оценивающего эффект приема алкоголя на риск развития того-или иного заболевания. Прием алкоголя связан со значительным числом негативных последствий для организма от заболеваний печени до развития онкопатологии, поэтому невозможно преднамеренно подвергать подобному риску людей в экспериментальной группе.

Также, МР анализ применяется в случае исследования заболеваний, возникающих во взрослом возрасте с точки зрения оценки влияния факторов риска, оказавших воздействие на индивида в детстве. В работе, опубликованной в 2020 году, Richardson и соавторы [38] использовали полиморфизмы генов, ассоциированные с избыточной массой тела детей чтобы оценить зависимость риска развития ряда заболеваний (ишемическая болезнь сердца, диабет 2 типа, рак молочной железы и рак предстательной железы) от антропометрических показателей в детском возрасте. В исследовании показано, что повышенный риск развития ишемической болезни сердца и диабета 2 типа у лиц, страдавших ожирением в детстве, значимо снижается при снижении массы тела во взрослом возрасте.

МР анализ может применяться для оценки экономического эффекта профилактики модифицируемых факторов риска на здравоохранение. Интересное примером было служит исследование, проведённое коллективом под руководством Dixon [25, 39], в котором авторы показали перспективы применения МР для оценки влияния избыточной массы тела на госпитальные расходы.

Перспективным является применение МР для валидации мишеней лекарственных препаратов (цис-Менделевская рандомизация) [40, 41], когда в качестве инструментальных переменных используются полиморфизмы генов, кодирующих белки-мишени того или иного лекарственного средства.

Пример применения и интерпретации результатов МР анализа

В работе Han и соавторов [42] метод Менделевской рандомизации на двух выборках применялся для оценки влияние С-реактивного белка на риск развития возрастной макулярной дегенерации (ВМД).  Исследователи провели полногеномное исследование ассоциаций концентрации С-реактивного белка в плазме крови на выборке из 418642 участников Британского биобанка. В результате было идентифицировано 526 полиморфных вариантов, которые объясняли 13% дисперсии С-реактивного белка, и эти варианты были далее использованы в качестве генетических инструментов. Следующим этапом было проведение полногеномного исследования ассоциаций возрастной макулярной дегенерации на выборке из 27301 участников международного консорциума по изучению генетики ВМД.  Полученные результаты анализа ассоциации (регрессионные коэффициенты) 526 вышеупомянутых полиморфных вариантов с риском развития различных форм ВМД использовались для проведения МР анализа. Было показано наличие значимой связи уровня С-реактивного белка с повышенным риском развития различных форм ВМД (ОШ от 1,15 до 1,52, p <0,05). Данное исследование, проведённое с применением генетической информации, предоставило убедительные доказательства того, что более высокие уровни циркулирующего СРБ ассоциированы к повышенным риском развития всех форм ВМД, что может говорить о причинно-значимой роли воспалительных процессов в патогенезе ВМД.

Заключение. В заключение, следует отметить, что Менделевская рандомизация является удобным инструментом в руках эпидемиолога, позволяющим в короткие сроки определить наличие причинно-следственной связи. Появление большого количества информации о генетических вариантах в эру полногеномных ассоциативных исследований значительно упрощает проведение МР анализа. Важно помнить, что в данном анализе оценивается влияние фактора риска «на протяжении всей жизни», а не срезовый, «одномоментный» эффект. Также, получение достоверных результатов МР-исследования зависит от выполнения ряда условий, таких как выбор валидных инструментальных переменных, проведение анализов чувствительности, оценки статистической мощности теста.

Информация о финансировании

Финансирование данной работы не проводилось.