Introduction. In practical medicine, medicines based on plants or their biologically active compounds play an important role for the treatment of chronic diseases of the nervous system, upper respiratory tract, gastrointestinal tract, skin and mucous, cardiovascular system and even for the treatment of cancer diseases [1]. This fact can be explained by a polycomponent composition, multitargeted action, and low toxicity of medicines belonging to this group.

In recent years, scientists from different countries have been expressing their interest in compounds obtained from plants as some valuable medicines based on biologically active compounds from plants had been found and introduced into clinical practice for the treatment of malaria, cancer diseases, Alzheimer's disease and some other severe diseases [2-4].

At the same time, new extraction technologies for different groups of compounds from plant raw material using different physical factors or phenomena are still discovered, often empirically without any theoretical base [5].

It should be noted that at the moment, there are no theoretical principles to describe the process of phytocompounds’ extraction based on adsorption-desorption concept. At the same time, a kinetic aspect of the extraction process has been more developed owing to the use of the molecular diffusion theory of matter [6], whereas a thermodynamic approach associated with equilibrium state of this process practically has not been developed yet.

Therefore, theoretical development of this aspect of the extraction process is an important task for further modeling and calculation of optimal conditions for extraction of biologically active compounds from the plant raw material.

Glycyrrhiza glabra L. and Glycyrrhiza uralensis Fisch. radices are the raw material used for production of some valuable biologically active compounds and medicines like Glycyrrhizae extract siccum (Glycyrrhizae radices syrup), glycyrrhizinic acid salts (Glycyram), flavonoids and chalcones (Licuroside, Flacarbinum), and some other products [7, 8].

Thus, the study of the distribution process of some biologically active compounds between Glycyrrhiza radices and the extractant is an important and justified task.

The aim of this work was to propose and test a theoretical model to describe the process of Licuroside and Glycyram distribution between the solid phase of Glycyrrhiza radices and the extractant.

Materials and methods

Plant raw material and chemicals

For studies, we used Glycyrrhiza radices (Liquorice roots) by “Krasnogorskleksredstva” company, Krasnogorsk, the Russian Federation, serial No 30417, best before 05/2018.

For extraction, we used plant raw material with particle size of 0.1-0.5 mm, and ethanol-water solution 70 % v/v was used as an extractant.

Qualitative and quantitative analyses of biologically active compounds were carried out with standard substances Licuroside and monoammonium glycyrrhizate (Glycyram) (the State Pharmacopoeia of Ukraine) and according to UV-spectra and retention times of compounds in the HPLC profile.

Method of extraction

The extraction process was carried out at temperatures of 4, 20, 40 and 60±1 ºС. Simple maceration during 24 hours was used. Distribution of BAS between the phases was studied at such ratios of mass plant raw material / extractant volume as 1:5, 1:10, 1:20, and 1:40. For this purpose, the plant raw material (exact weight) and extractant were placed into a hermetic bottle and stored in the thermostat or refrigerator for 24 hours with periodic shaking of its content, and after the extraction, it was weighed again, taking into account the evaporated extractant.

Determination of Licuroside and Glycyram in the extracts and plant raw material was carried out by HPLC analysis.

HPLC analysis

HPLC analysis was carried out with chromatograph Agilent Technologies 1200 Infinity, USA. Chromatographic conditions of the extracts obtained were described in another publication [9]. Determination on diode array detector was carried out at 360 nm for Licuroside and 258 nm for Glycyram.

Theoretical part

To construct the simplest mathematical model of BAS distribution between the extractant and plant raw material matrix, we used the law of conservation of matter and Henry’s adsorption law. Therein, the following assumptions were used: the system attains equilibrium, the volume of extractant in the system is practically not changed, the value of BAS adsorption on the plant raw material matrix conforms to the Henry’s law. Under such assumptions, distribution of BAS in the extraction system can be described by equation (1) that exhibits material balance of the compound in the closed system [10]:

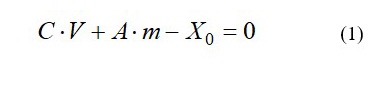
where C is equilibrium concentration BAS in the extract, g/ml;

V is volume of the extractant in the extraction system, mL;

A is BAS concentration on the plant raw material matrix, g/g matrix;

m is mass of plant raw material matrix, g;

X₀is BAS content in the extraction system, g.

The adsorption value for compound (A) on the plant’s matrix can be described by equations (2) and (3):

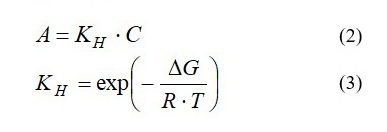
where K_H is distribution constant of the compound (Henry’s constant), mL/g plant’s matrix;

ΔG is the change of free Gibbs energy, J/mole;

R is gas constant, 8.314 J/mole·K;

T is absolute temperature of the extraction system, K.

From equations (1) and (2), we can come to equation (4) [11, 12]:

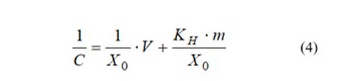
As it can be seen from equation (4), experimental data should be well described by linear dependency in coordinates 1/С=f(V). Therein, the value of ΔG can be found with equation (5):

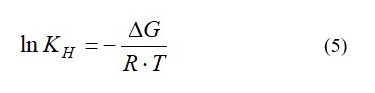
Regression analysis was carried out in MS Excel 2010 add-in “Data Analysis”.

Results and discussion. Main parameters of plant raw material are presented in Table 1.

Fig. 1 and 2 present the results of data processing with equation (4) after a series of experiments at different temperatures and ratios of plant raw material / extractant.

Main pharmacognostic parameters of Glycyrrhiza radices

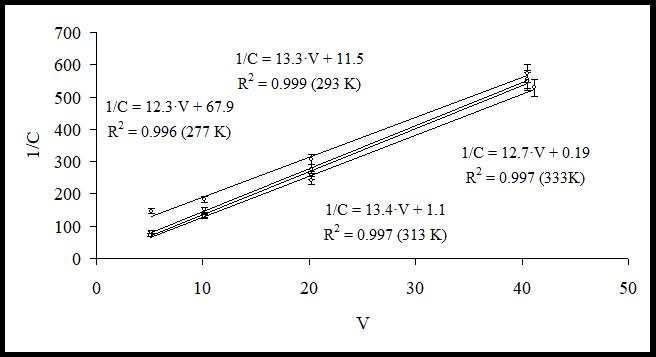
Fig. 1. Experimental data and regression lines for Glycyram

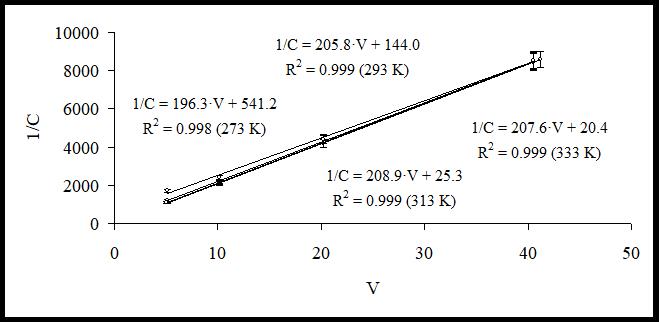
Fig. 2. Experimental data and regression lines for Licuroside

As it can be seen from the graphs presented in Fig. 1 and 2, experimental data are described well by the suggested theoretical model and have linear dependency as predicted by equation (4) (determination coefficient is equal to R²˃0.99). After that, using the constants obtained in regression equations, we calculated the distribution constant for compound (K_H) and built its dependency on the temperature in coordinates (lnK_H=f(1/T)). The graphs of the regression equations obtained for Licuroside and Glycyram are presented in Fig. 3.

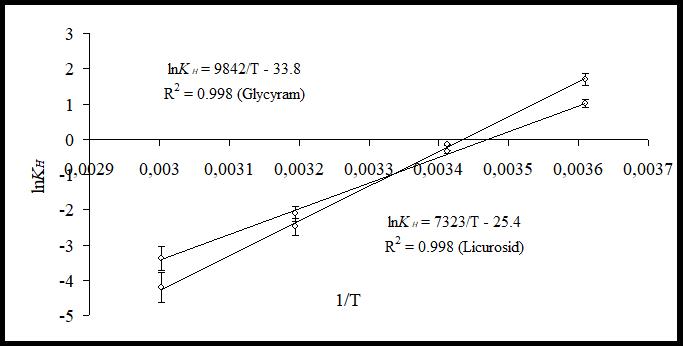
Fig. 3. Dependency of distribution constant K_H on temperature for Licuroside and Glycyram

As it can be seen from the graphs presented in Fig. 3, the dependency for compound’s distribution constant (K_H) on temperature (T) is also described well by the suggested equation (5), with determination coefficient that equals R²˃0.99. Then, by means of mathematical transformation, we can calculate constants (ΔG, k₁) from the regression coefficients. Table 2 presents the value of constants for plant raw material used in the experiment.

Table 2

Values of theoretical constants